Understanding Quantum Computing
A Gentle Introduction
When people first encounter quantum computing, they usually hear about how it will solve problems that would take regular computers thousands of years. But what actually makes quantum computers different? And why can’t we just build faster regular machines instead?
I’ll start with the basics: what a qubit is and how it differs from a normal bit. Then we’ll build up to superposition, entanglement, and interference. These are the three ideas that make quantum computing work.
Bit vs Qubit
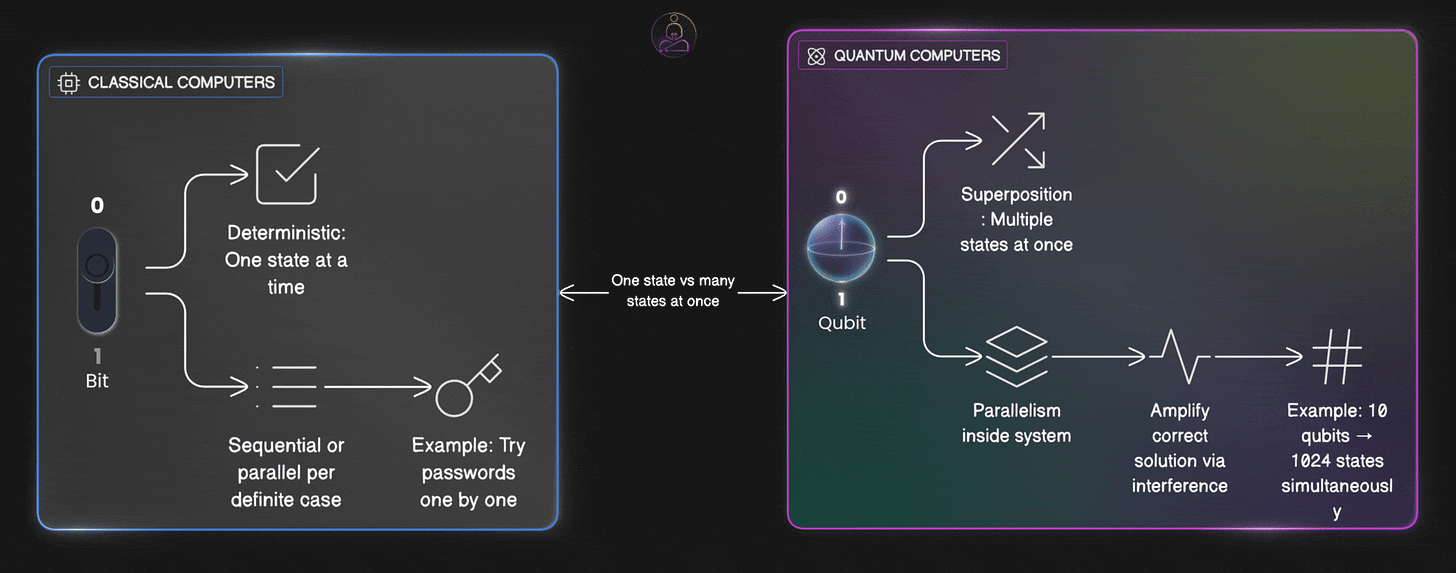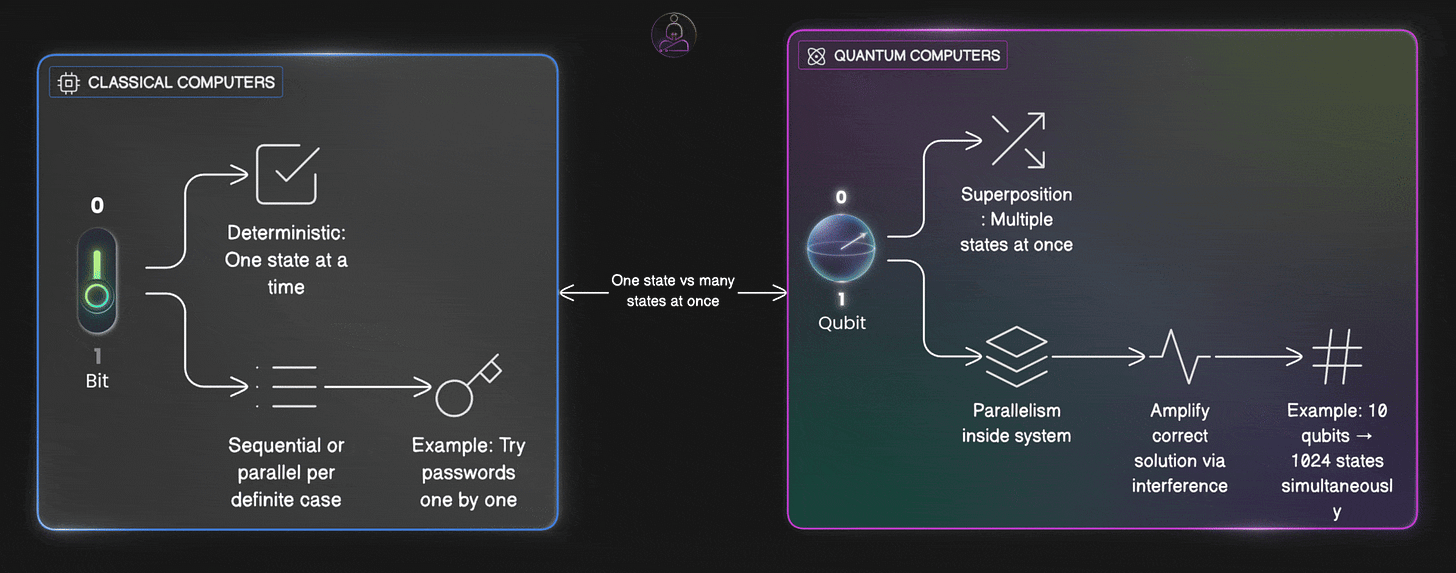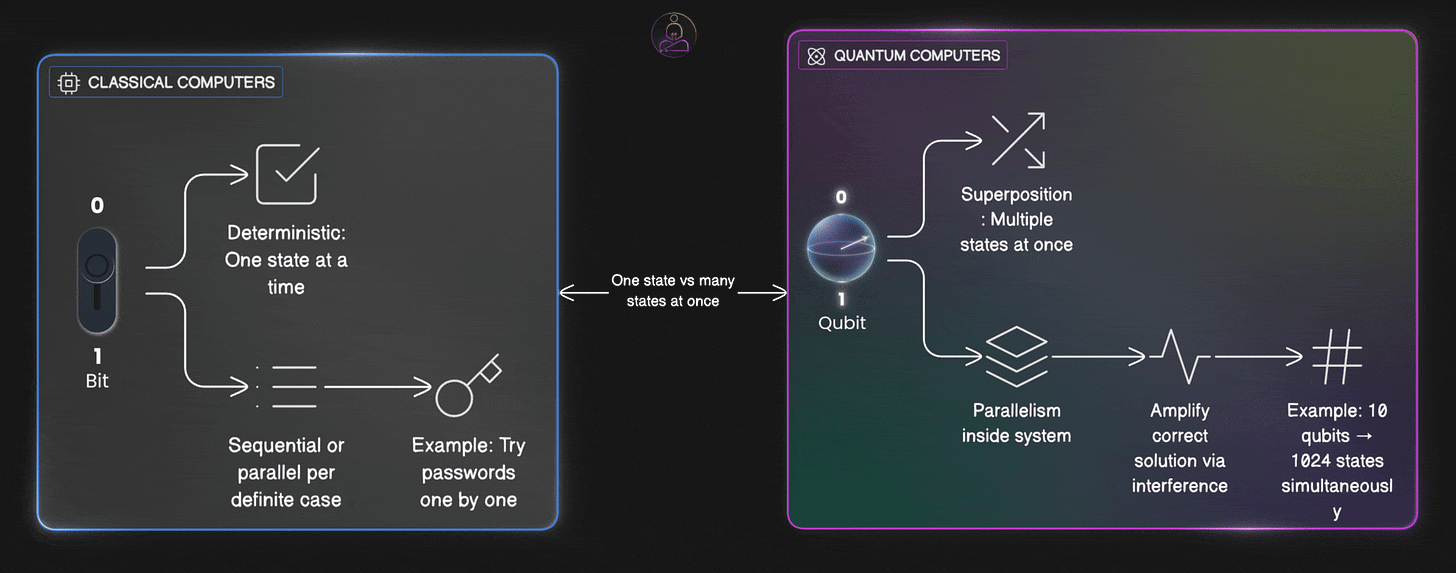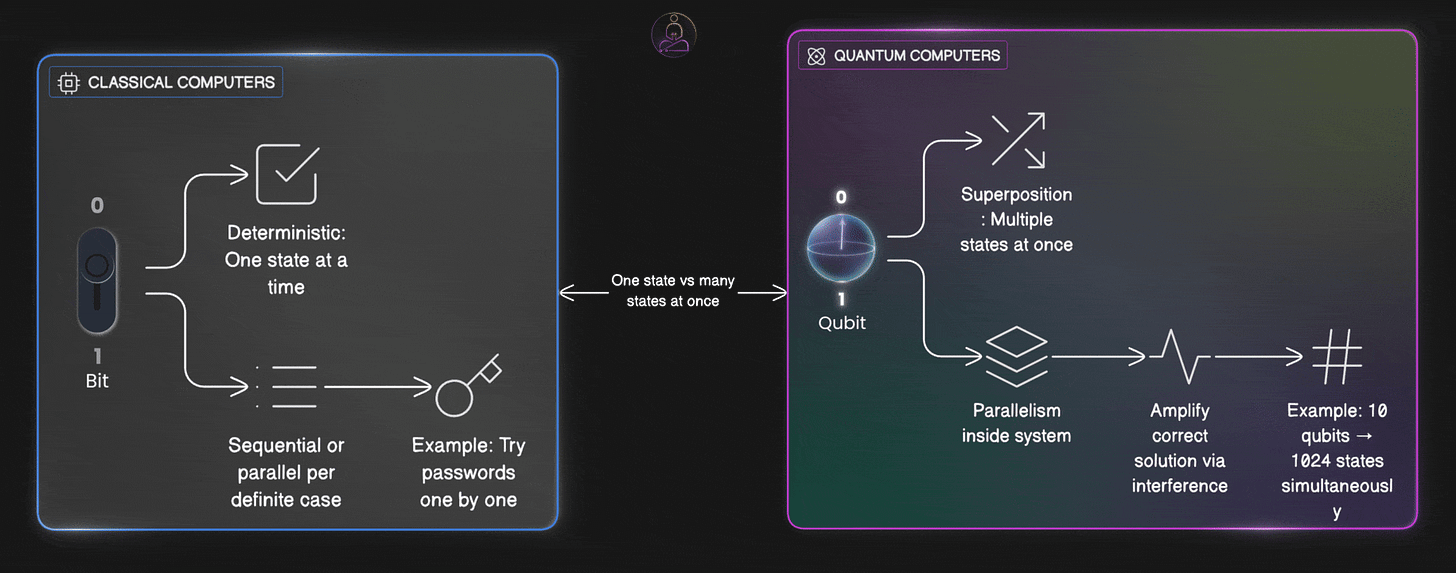
Before we get into quantum stuff, let’s talk about what we already know. A classical bit is the basic unit of information in regular computing. It’s binary: at any moment, it’s either 0 or 1. No ambiguity, no in-between.
Think of a bit like a coin lying flat on a table. It shows either heads (0) or tails (1). When you compute something, you flip these bits around using logic gates like AND, OR, and NOT. One definite state becomes another definite state.
Here’s what this means in practice: if you want to check a million different possibilities, you have to go through them one by one. Even if you split the work across multiple processors, each one is still checking individual cases, one at a time. Each operation takes one specific input and gives you one specific output.
A qubit (quantum bit) is different. Instead of being locked into 0 or 1, a qubit can exist in what we call superposition. Think of it as a blend of both states at the same time.
If a classical bit is a coin lying flat showing heads or tails, a qubit is like a coin spinning in the air. While it spins, it hasn’t committed to either outcome. It has some chance of landing heads and some chance of landing tails. That spread of chances is its quantum state.
A qubit might be 70% likely to end up as 0 and 30% likely to be 1. Or it could be a perfect 50/50 split. The important thing is that until you actually look at it, the qubit represents this blend of possibilities. It’s not that we just don’t know which one it is. The qubit genuinely holds both at once.
When you do check the qubit (like catching that spinning coin), the superposition collapses. The qubit picks one outcome: either 0 or 1. You never see it as both. The moment you look, it commits.
Classical vs Quantum: A Tale of Two Computers
The difference between regular computers and quantum computers isn’t just about speed. It’s about how they represent and work with information.
Regular computers operate step by step. Each bit stores exactly one value. If you need to test multiple possibilities, like trying different passwords or searching a huge database, you check them one at a time. Sure, you can split the work across multiple cores, but each core is still looking at individual cases. The basic process is sequential.
Quantum computers work differently because of superposition. They can represent many possibilities at once. Here’s where it gets interesting:
1 qubit in superposition can represent 2 states at the same time
2 qubits can represent 4 states (00, 01, 10, 11) at once
3 qubits can represent 8 states
10 qubits can represent 1,024 states
n qubits can represent 2^n states
This exponential growth is wild. It means a quantum system can handle all these combinations simultaneously within a single quantum state.
But here’s something that confuses people.
Why One Qubit Isn’t the Same as Two Regular Bits
You might be thinking: “If one qubit can be 0 or 1 like a regular bit, isn’t one qubit basically two bits?”
Not quite. Two regular bits give you four possible combinations (00, 01, 10, 11), but they can only hold one of those at any moment. Maybe it’s 10 right now. That’s it. One definite state.
One qubit changes everything. It exists in a superposition of 0 and 1 at the same time. Two qubits can represent all four combinations at once. Three qubits hold eight states simultaneously.
Regular bits store one answer. Qubits carry whole libraries of possibilities all at once. That’s the real difference.
Visualizing Qubit States: The Bloch Sphere
To understand how qubits work, physicists use something called the Bloch sphere. It’s basically a globe that maps all possible states of a single qubit.
At the top of this globe, you have the pure 0 state. At the bottom, the pure 1 state. A regular bit could only sit at one of these two spots.
But a qubit can point anywhere on the surface of this sphere. Tilt it slightly toward the bottom and it’s mostly 1 with a small chance of 0. Put it on the equator and it’s a perfect 50/50 mix. Every point on the sphere represents a valid quantum state with different odds of measuring 0 or 1.
This isn’t just a pretty picture. It’s how we think about changing qubits. To move a qubit to a different state, we rotate it around the sphere using operations called quantum gates.
Superposition: Holding Multiple Possibilities
Superposition is the ability of a qubit to be in a combination of states at the same time. It’s not that we don’t know which state it’s in (that would just be regular uncertainty). The qubit actually holds both possibilities at once, each with a certain probability.
Think back to that coin spinning in the air. The qubit isn’t secretly heads or tails while we’re not looking. It’s genuinely in a state that contains both outcomes. Only when we check does it collapse into one answer.
When you have several qubits in superposition together, you can represent a huge space of possibilities. Imagine you want to test millions of different coin flips. A regular computer would check them one by one. A quantum computer, because each qubit can be in superposition, handles all those tests in parallel inside one system.
This parallel processing doesn’t come from having more hardware. It comes from the quantum properties of the qubits themselves.
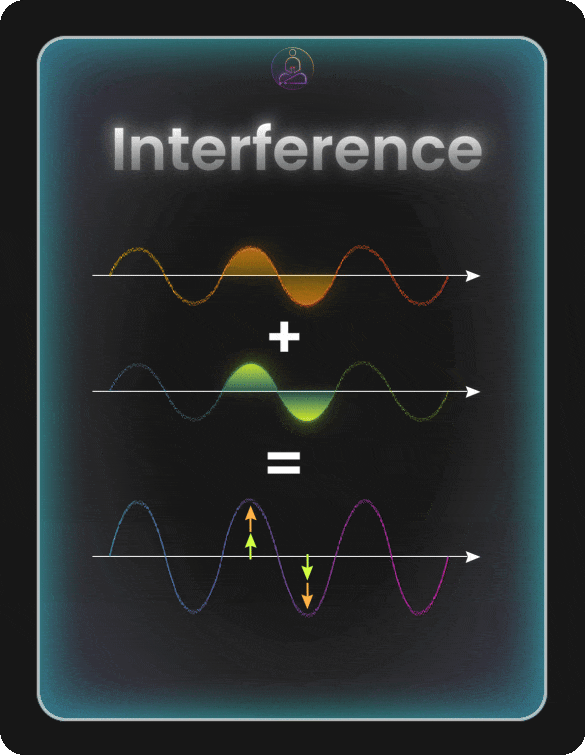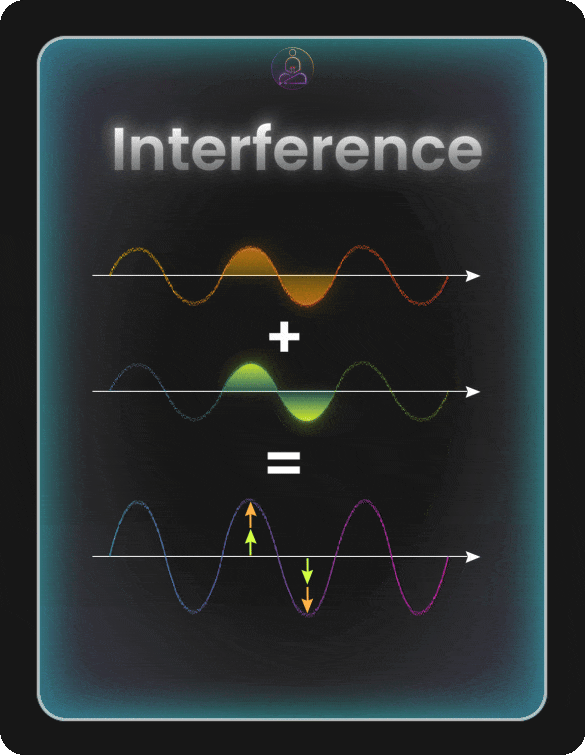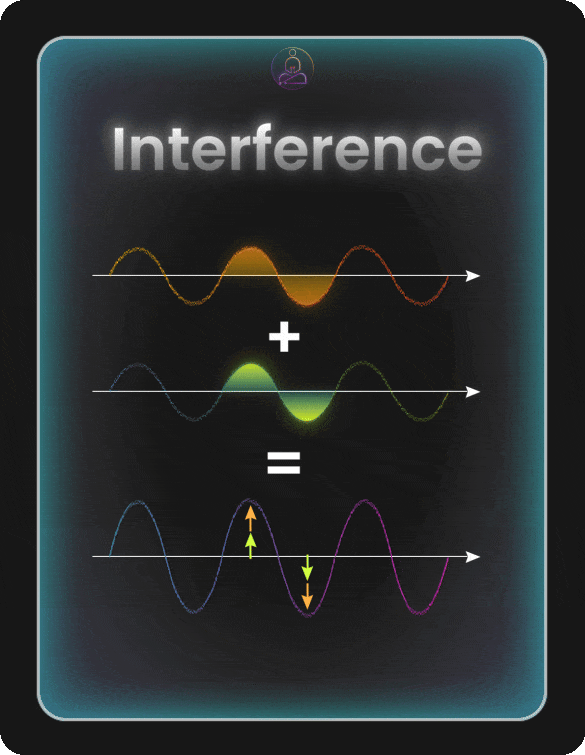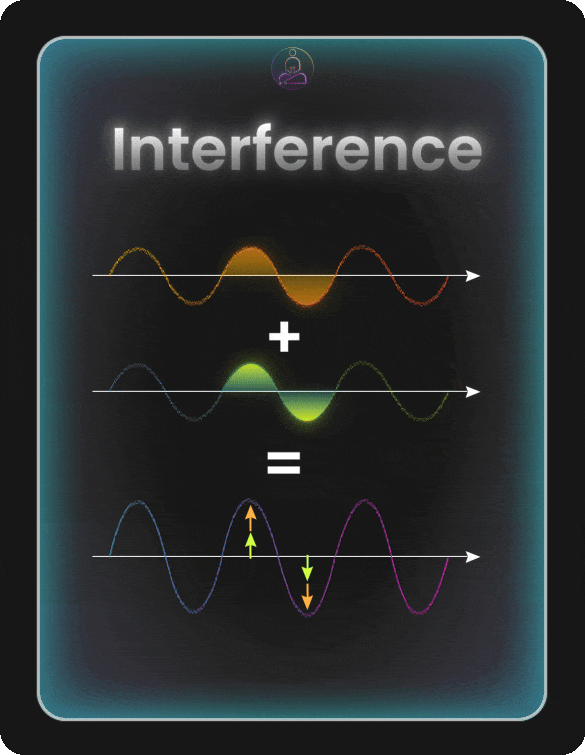
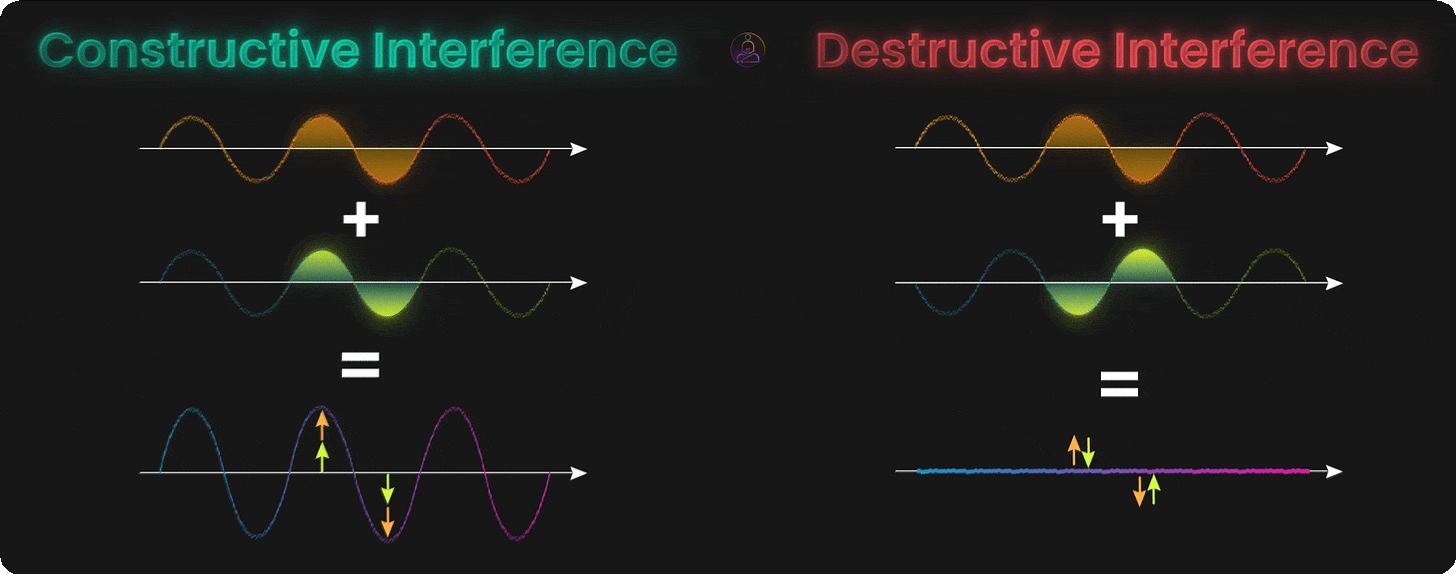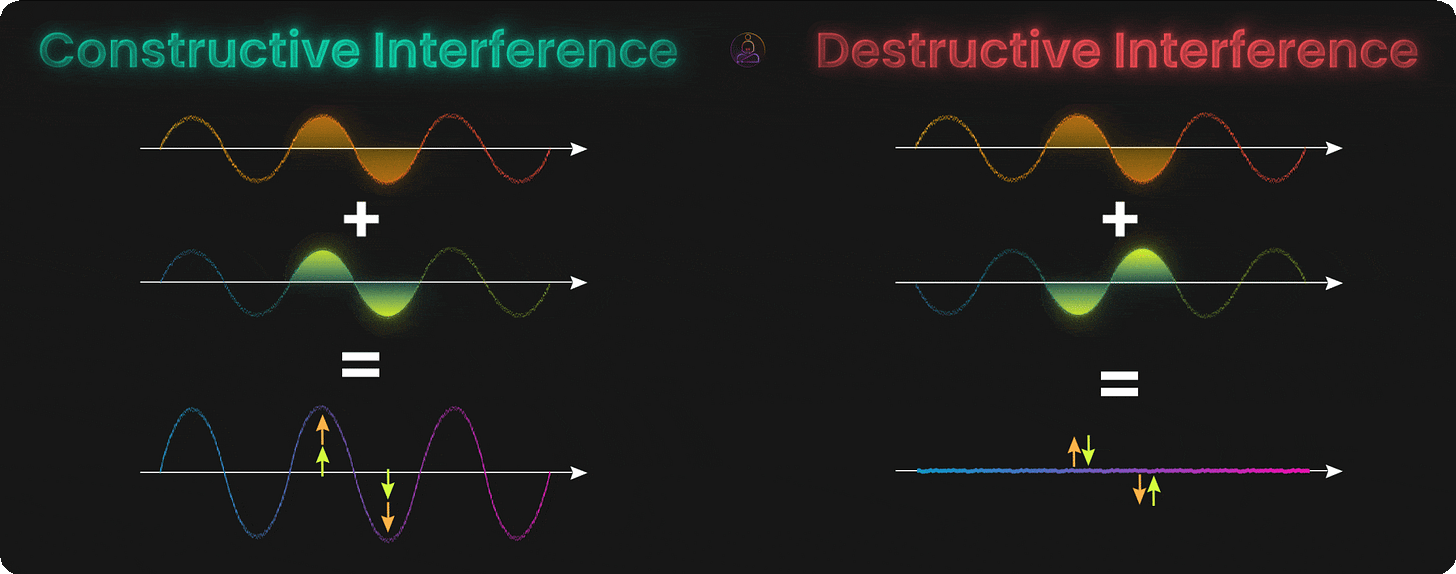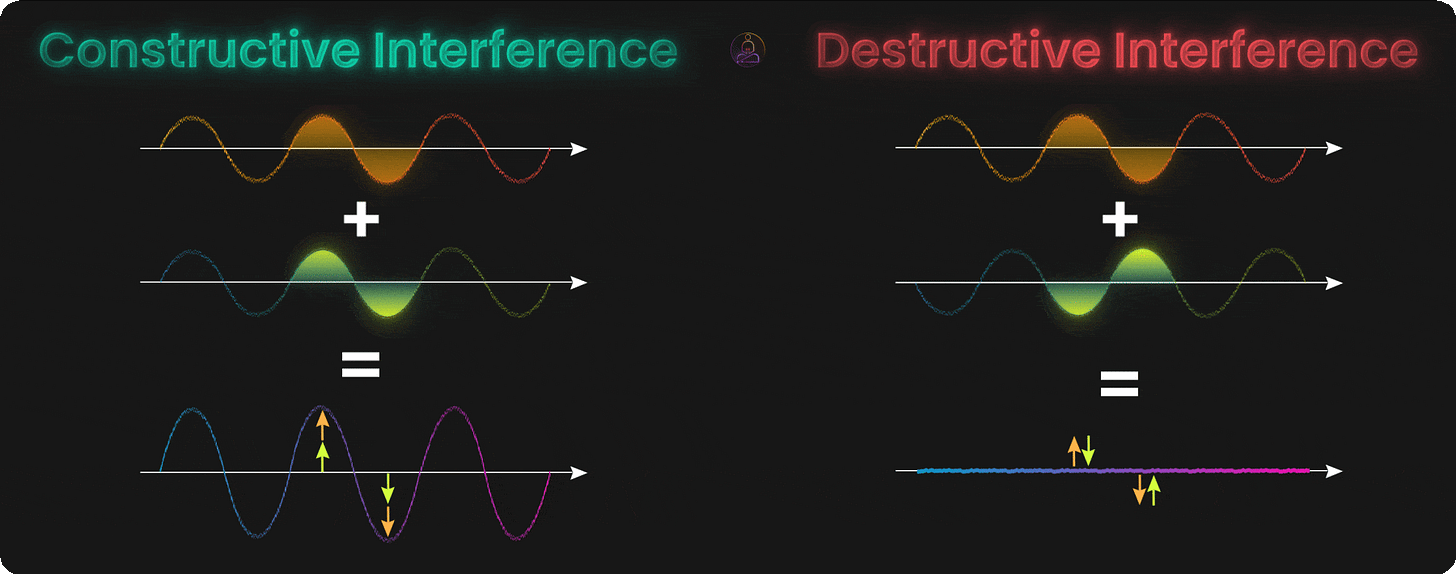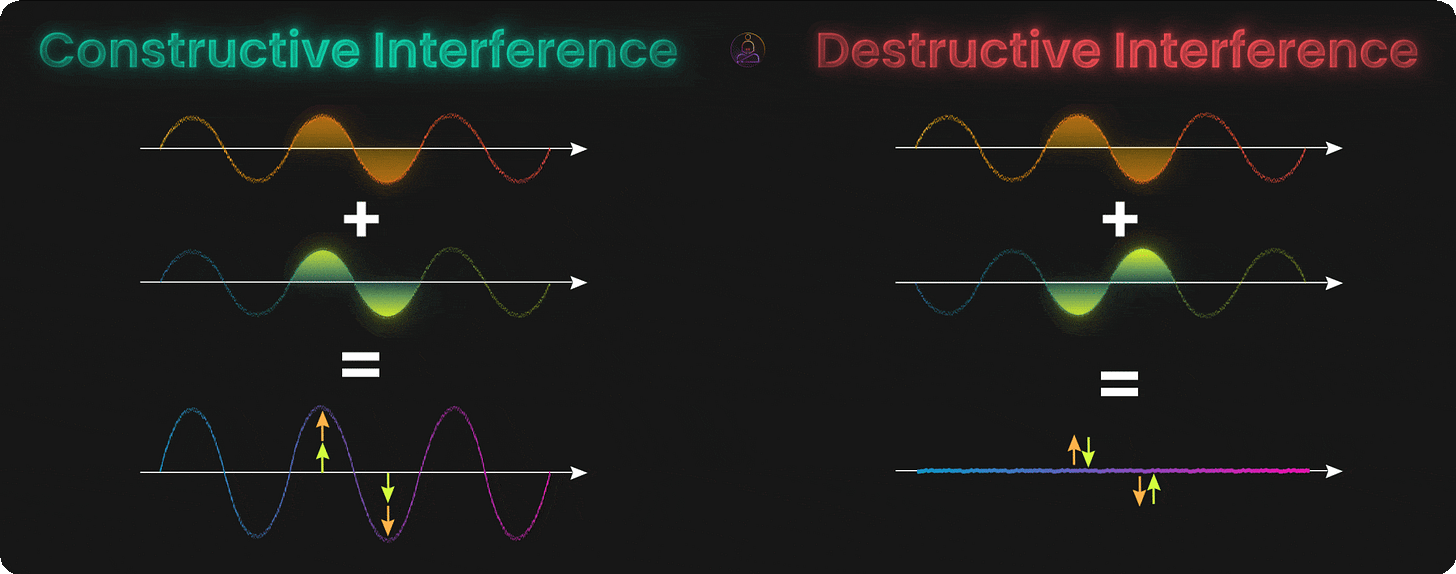
Interference: Amplifying the Right Answer
Having qubits explore many possibilities at once sounds great. But if we just measured them right away, we’d get one random outcome from all those possibilities. The real magic comes from interference.
Think of interference like ripples on a pond. When two ripples meet, sometimes they add up to make a bigger wave (constructive interference). Sometimes they cancel each other out and leave flat water (destructive interference).
Quantum states work the same way. Their probabilities can build up or cancel out depending on how we manipulate them. This is the secret of quantum algorithms: we set things up so wrong answers cancel out, while the correct answer gets amplified.
When you finally measure the qubits, you still only see one result, like picking one book from a library. But we’ve arranged the math so the wrong answers have mostly cancelled themselves out. The correct answer becomes the most likely thing to show up when we measure.
Constructive interference happens when quantum states line up and reinforce each other. The probabilities add up, making certain outcomes more likely. This is what we want for the correct answer.
Destructive interference happens when quantum states work against each other and cancel out. The probabilities shrink or disappear. This is what we want for wrong answers.
Quantum algorithms are carefully designed routines that use interference to push probability toward the solution we’re looking for.
Quantum Gates: Choreographing Probability
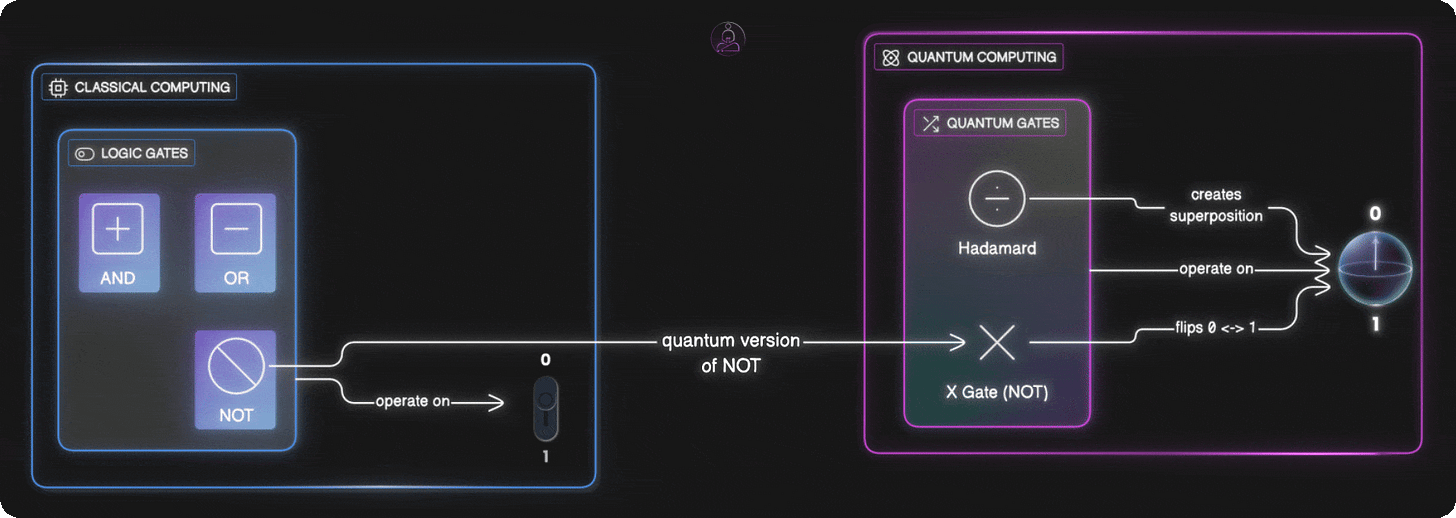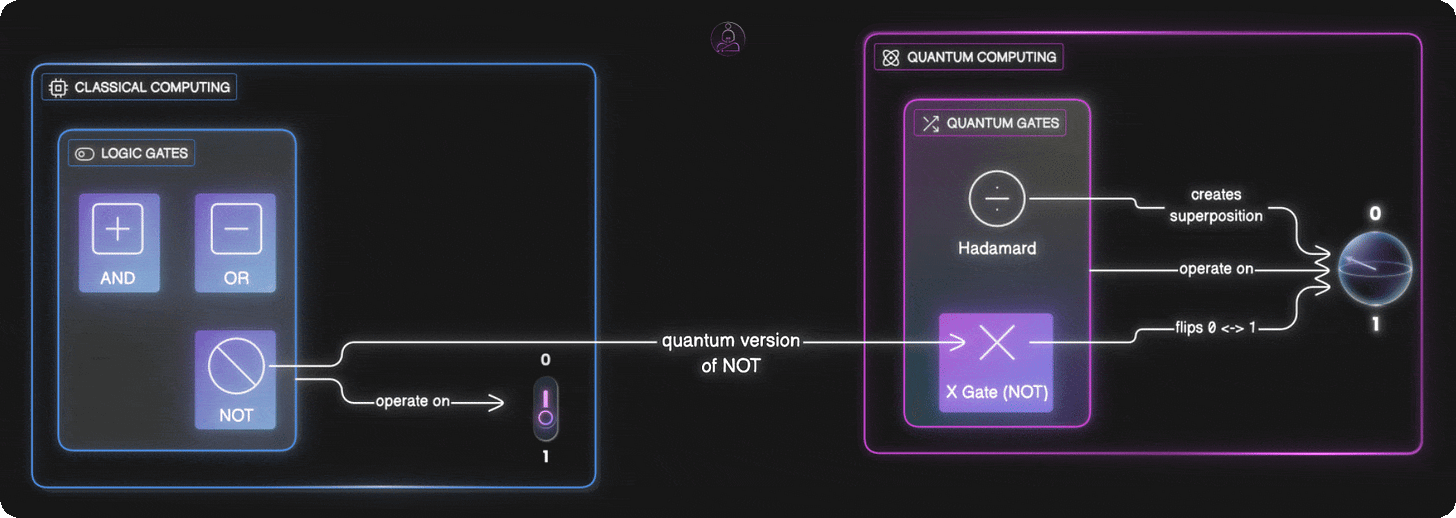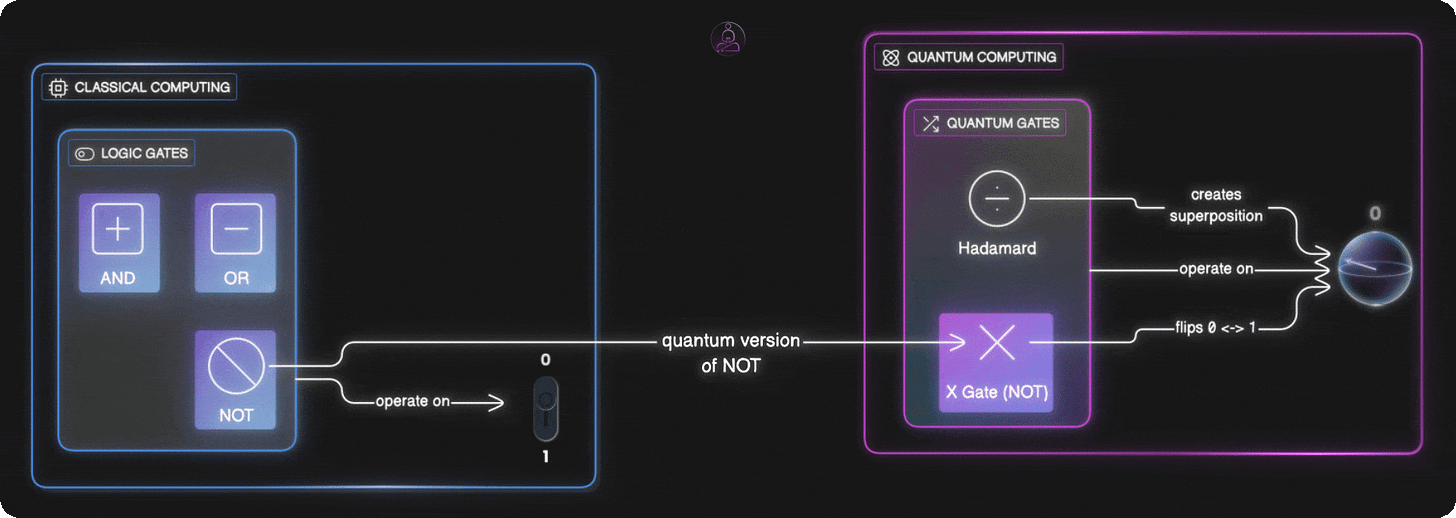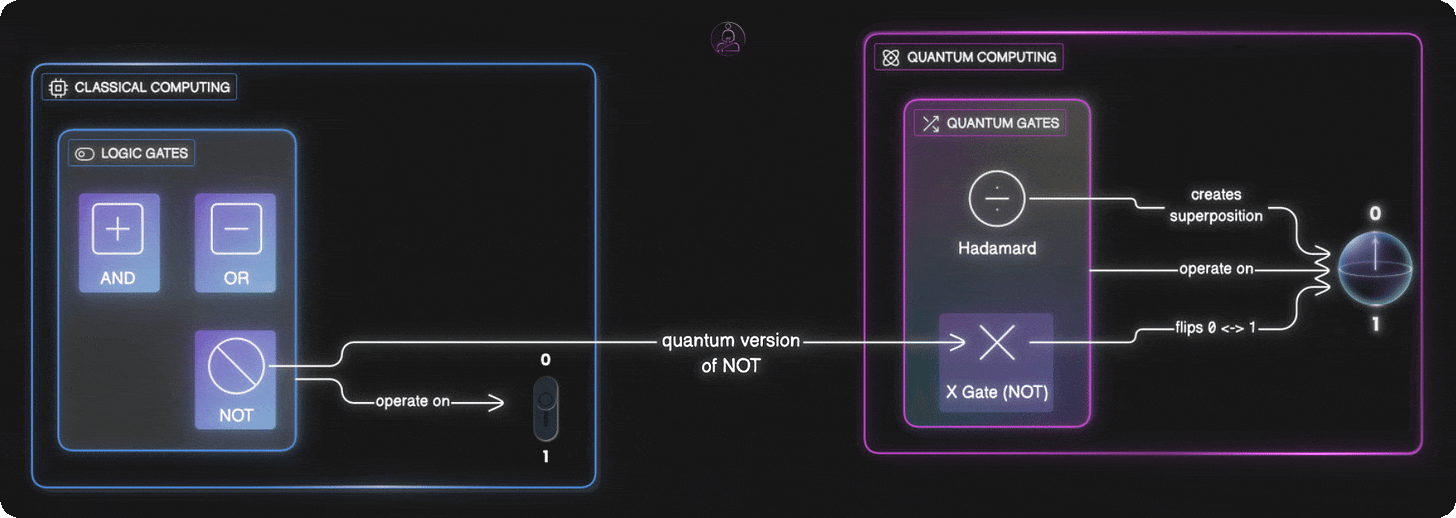
Just as regular computers use logic gates (AND, OR, NOT) to work with bits, quantum computers use quantum gates to work with qubits. But instead of flipping between definite values, quantum gates rotate qubits around the Bloch sphere, changing their probabilities.
Classical Gates as a Baseline
In regular computing, a gate like NOT just flips a bit. If it’s 0, it becomes 1. If it’s 1, it becomes 0. An AND gate takes two bits and gives you 1 only if both inputs are 1. These operations are predictable and definite.
Quantum Gates: Rotation and Mixing
Quantum gates are different. They transform a qubit’s state by rotating it to a different point on the Bloch sphere.
The X gate is the quantum version of NOT. If a qubit is in state 0, applying X rotates it to 1. If it’s in 1, X rotates it to 0. Simple flip, just like the regular NOT gate.
The Hadamard gate is more interesting. It doesn’t just flip. It creates superposition. If a qubit starts in the definite 0 state (top of the Bloch sphere), the Hadamard gate rotates it to the equator, creating a perfect 50/50 mix of 0 and 1.
Going back to our coin analogy, it’s like taking a coin lying flat showing heads and giving it a perfect spin so it’s equally likely to land heads or tails.
This is where the magic happens. By stacking many quantum gates in a row, we control how qubits rotate and tilt, building up complex probability patterns. These sequences of gates form quantum circuits. They’re like choreographed dances for probabilities, steering the qubits toward the answers we want.
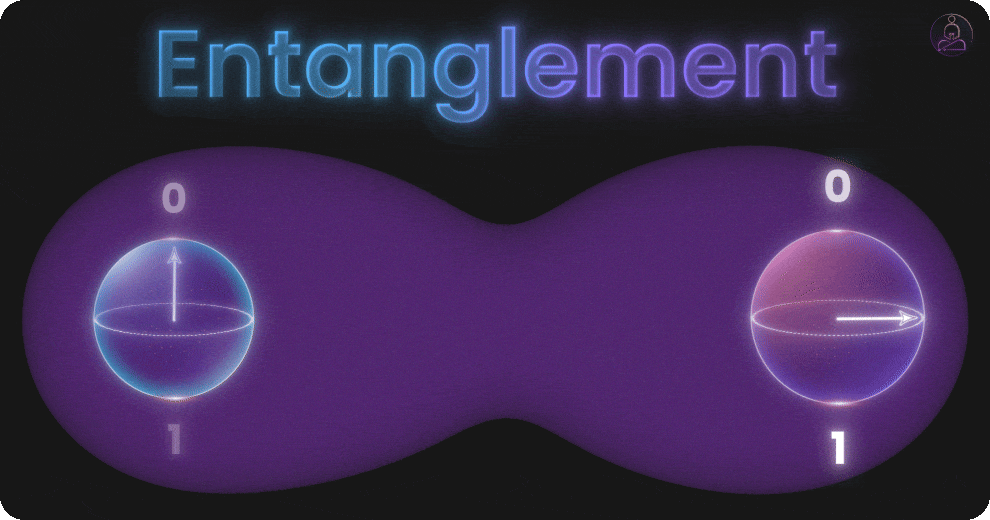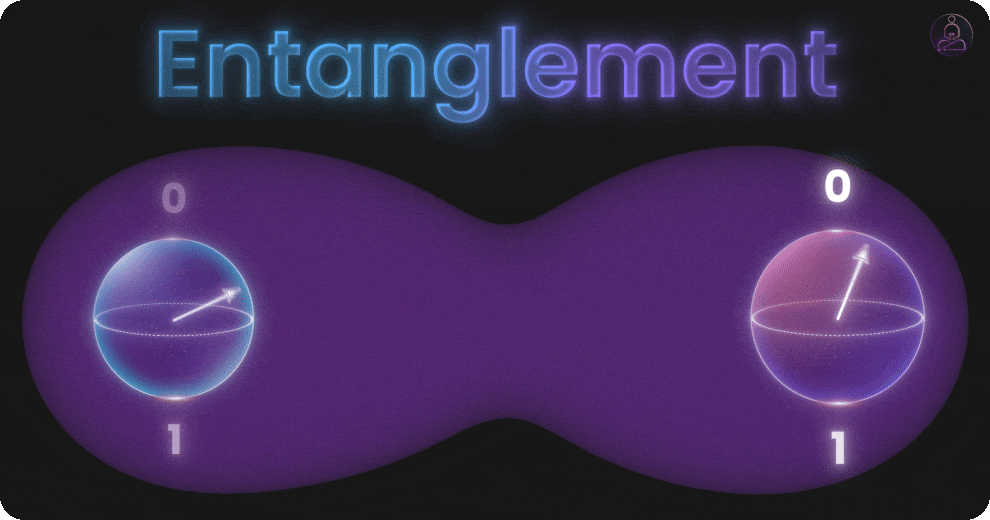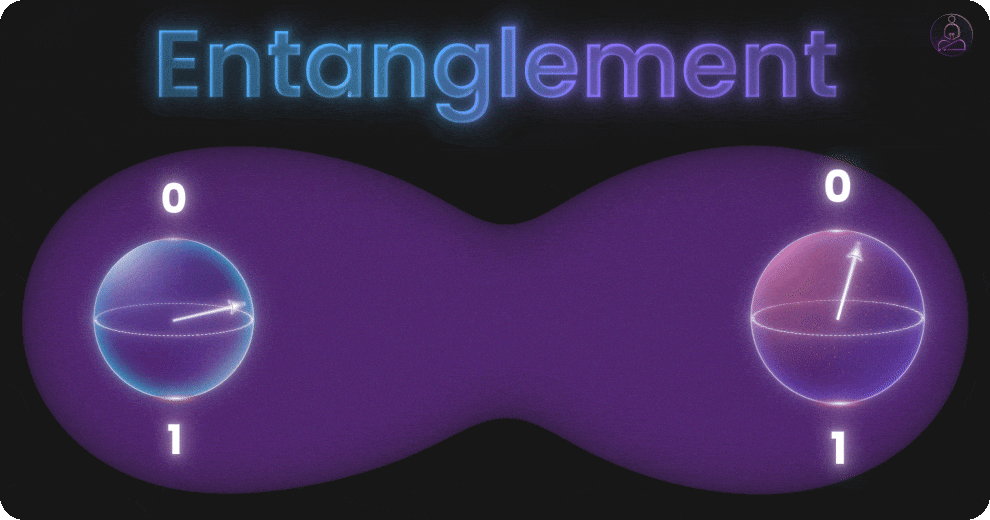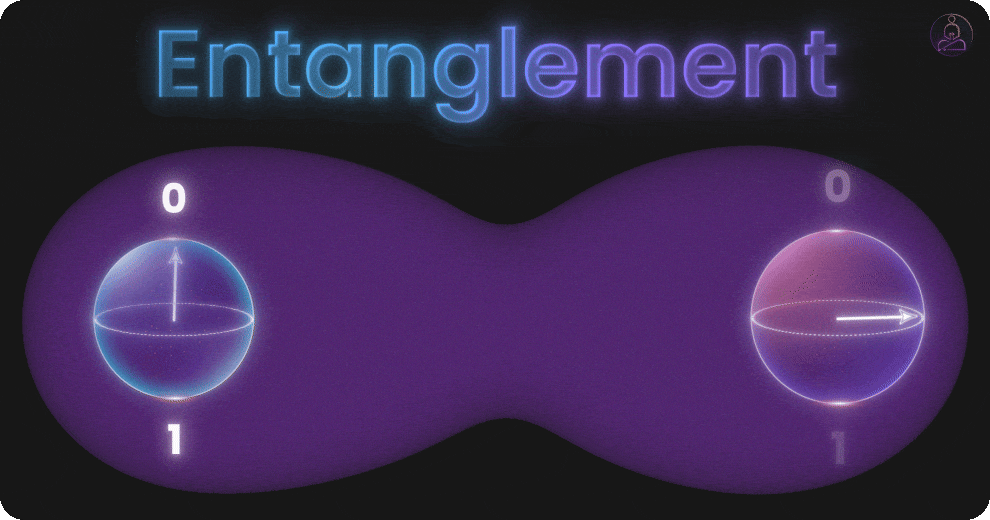
Entanglement: Qubits Working in Harmony
So far we’ve talked about individual qubits and how superposition lets each one represent multiple possibilities. But the real power shows up when qubits start working together through entanglement.
Entanglement is a special connection between qubits. When two qubits are entangled, their states become linked. If you check one, you instantly know something about the other, even if they’re far apart.
This isn’t because they’re sending signals to each other. There’s no hidden communication happening. It’s just how quantum mechanics works.
Einstein called it “spooky action at a distance” because it seemed so strange.
But entanglement is real, proven in experiments, and completely essential to quantum computing. With entanglement, a group of qubits can coordinate in ways regular bits never could. They don’t just work independently. They act as one unified system where the state of one qubit depends on the state of others.
Superposition Plus Entanglement Equals Quantum Power
Here’s where everything comes together. Let’s compare:
Two regular bits can store one of four possible values (00, 01, 10, 11) at any time. If you want to work with all four, you process them separately.
Two qubits in superposition can represent all four values at the same time until you measure them. But that alone isn’t enough for quantum advantage.
When those two qubits are entangled in the right way, quantum algorithms can use their combined state to do computations that consider multiple inputs at once. By using interference, we amplify correct answers and cancel out wrong ones across this entangled superposition.
Scale this up. Ten entangled qubits in superposition can represent 1,024 states at once. A hundred qubits can represent more states than there are atoms in the observable universe. Through interference, quantum algorithms can navigate this massive space efficiently, finding solutions that would take regular computers forever.
Putting It All Together
Quantum computing rests on three pillars:
Superposition lets each qubit explore many possibilities at the same time, giving quantum computers massive parallelism inside a single system.
Entanglement ties qubits together so they work in harmony, creating connections impossible for regular bits.
Interference lets us design computations where wrong answers cancel out and correct answers build up, steering the system toward solutions.
When you combine these three things (superposition to hold many states at once, entanglement to coordinate qubits, and interference to boost the right outcome), you get quantum computers that can handle certain problems incredibly efficiently.
Notice I said “certain problems.” Quantum computers aren’t faster than regular computers at everything. They excel at specific tasks where quantum interference helps, like factoring large numbers, searching unsorted databases, simulating quantum systems, and solving optimization problems. For most everyday computing, regular computers work just fine and are much easier to build and maintain.
Looking Ahead
We’ve covered the basic ideas that make quantum computing work: qubits, superposition, interference, quantum gates, and entanglement. These aren’t just theoretical concepts. They’re the building blocks that let quantum algorithms solve problems regular computers struggle with.
In the next post, we’ll look at quantum algorithms. These are the actual procedures that use these quantum phenomena to deliver real advantages. We’ll explore algorithms like Grover’s search and Shor’s factoring, see how they use interference and entanglement to beat their regular counterparts, and talk about what kinds of real problems quantum computing might help us solve.
Thanks for reading. If you have questions or want me to clarify anything, let me know.





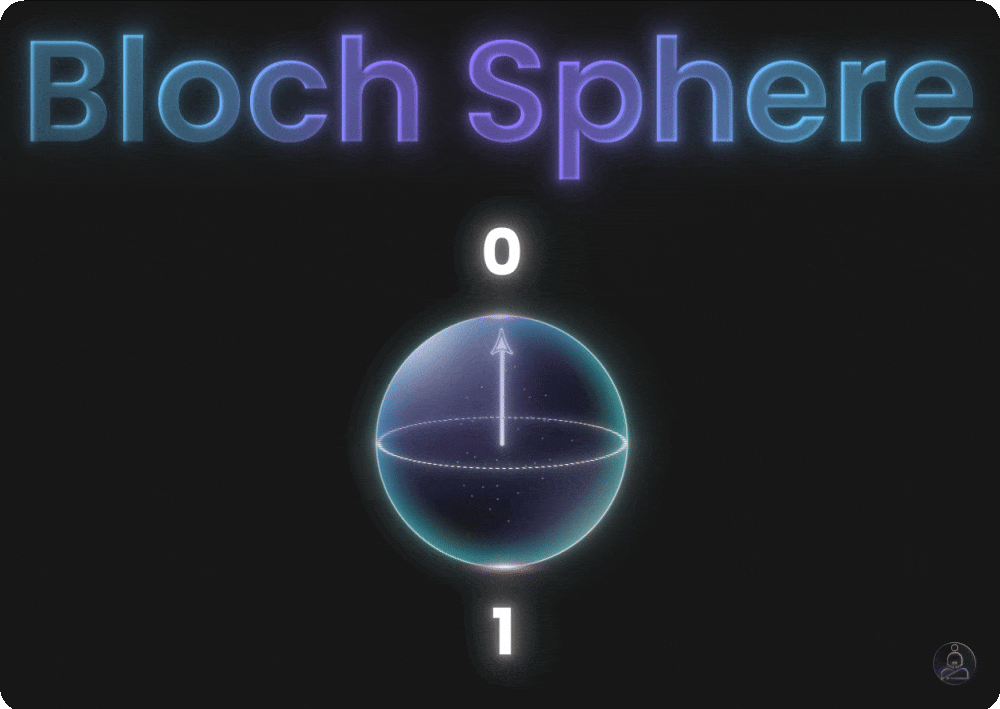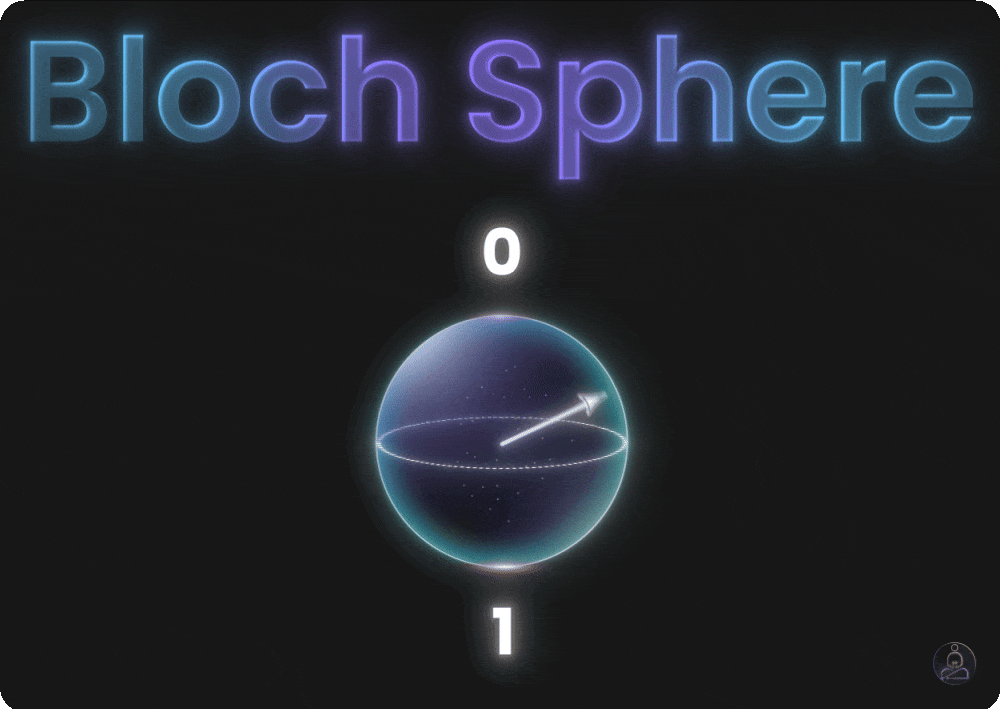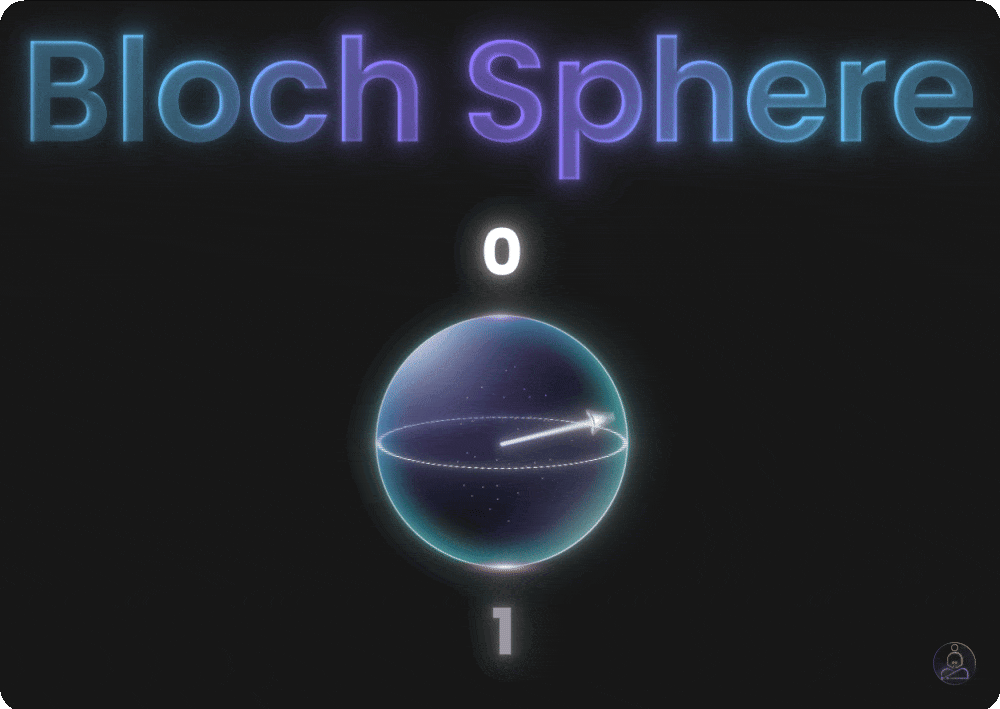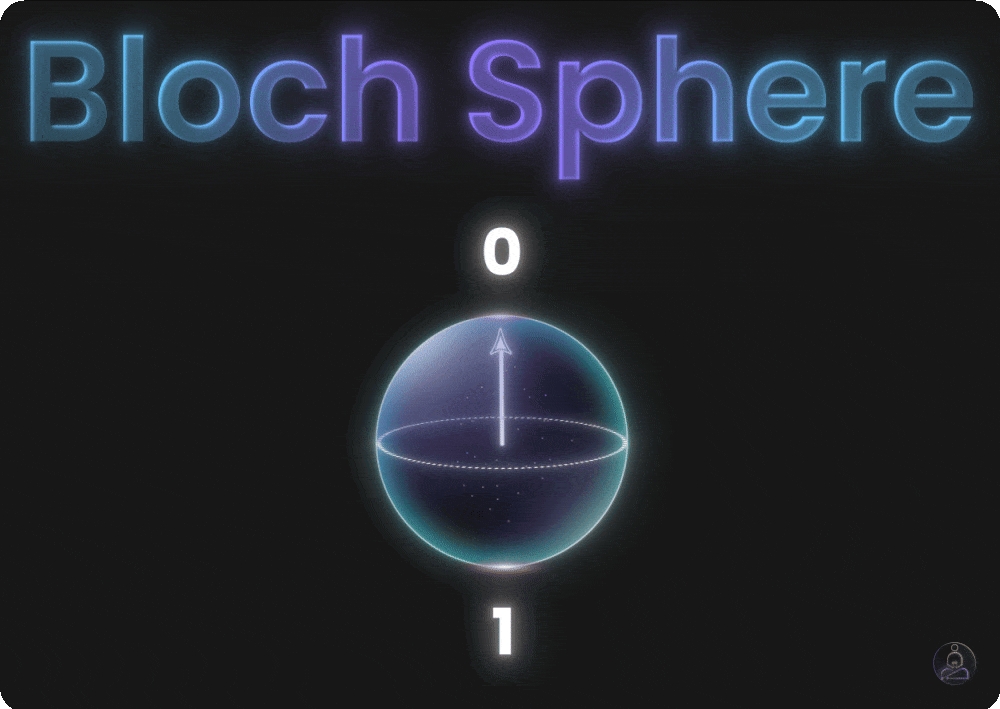


This is such a clear explination of quantum computing basics! The Bloch sphere visualization really helped it click for me. I've always struggled with understanding why superposition isnt just probabilty in disguise, but the way you describe it as genuinely holding both states until measurement makes more sense now. The interference section was particulary useful, the pond ripple analogy is great. Looking forward to the next post on quantum algorithms!
thaks for start writing blog, it is more effective way of learning for me. and also thanks for making quality content on youtube that is very helpful for me.